椭圆的定义与性质

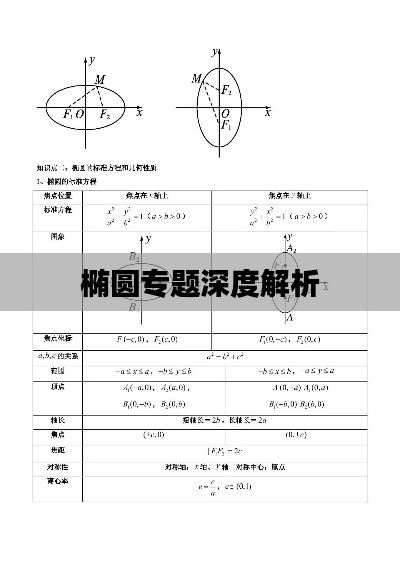
椭圆，作为一种常见的几何图形，具有独特的性质和应用，在平面内，椭圆可以定义为到两个定点（称为焦点）的距离之和等于常数的点的轨迹，这两个焦点位于椭圆的对称轴上，且椭圆关于这些轴具有对称性，椭圆的性质包括焦点到椭圆上任意一点的距离之和恒定，以及长轴和短轴的长度关系等。

椭圆的方程

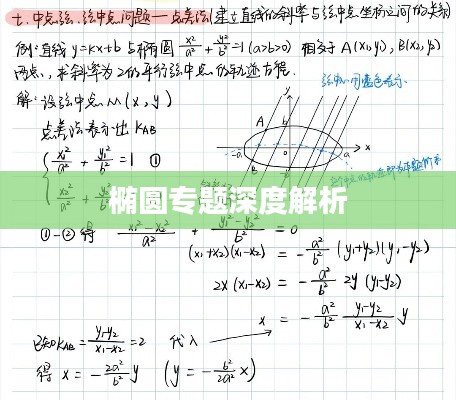
椭圆方程是描述椭圆形状和位置的重要工具，在平面直角坐标系中，椭圆的标准方程可以表示为：

x²/a² + y²/b² = 1

其中a和b分别表示椭圆的长半轴和短半轴的长度，这些值决定了椭圆的形状和大小，通过调整a和b的值，我们可以得到不同形态的椭圆。

椭圆的参数方程

椭圆的参数方程是一种描述椭圆上任意一点位置的另一种方式，参数方程允许我们更灵活地描述椭圆上的点，特别是在需要描述椭圆上点的运动轨迹时，椭圆的参数方程通常表示为：

x = a×cosθ

y = b×sinθ

是参数，表示椭圆上点的位置，通过改变θ的值，我们可以在椭圆上找到不同的点。

椭圆的焦点与焦距

椭圆的焦点是椭圆长轴的两个端点，也是椭圆对称轴的交点，焦距是焦点之间的距离，它与椭圆的长半轴和短半轴有关，焦距的公式为：c² = a² - b²，其中c表示焦距，了解焦点的位置和焦距的大小对于理解椭圆的性质和应用非常重要。

椭圆的应用

椭圆在生活和科学中有着广泛的应用，行星的运动轨迹可以近似为椭圆，这有助于我们预测行星的位置和运动，椭圆在光学、电磁学、工程学等领域也有广泛的应用，透镜的形状被设计成椭圆形，以优化光的聚焦效果。

椭圆的专题讲解实例

为了更好地理解椭圆，我们可以通过具体的实例来进行讲解，我们可以研究一个行星绕太阳运动的轨道，这个轨道可以近似为一个椭圆，我们可以讨论这个行星的轨道形状（即椭圆形状），以及它如何随着时间在轨道上移动，我们还可以讨论这个行星的轨道参数，如半长轴、半短轴和离心率等，以更好地理解其运动规律，通过这些实例，我们可以将理论知识与实际应用相结合，更好地掌握椭圆的性质和应用。

本文详细讲解了椭圆的定义、性质、方程、参数方程、焦点与焦距以及应用，通过专题讲解实例，我们将理论知识与实际应用相结合，以更好地理解和掌握椭圆，椭圆作为一种重要的几何图形，在生活和科学中有着广泛的应用，因此掌握椭圆的相关知识对于理解和解决现实问题具有重要意义。