圆锥作为一种常见的几何体，其侧面展开图的研究对于培养学生的空间想象能力和数学思维能力具有重要意义，本文将围绕“圆锥侧面展开图”这一主题，进行专题训练，帮助学生更好地理解和掌握相关知识。

圆锥侧面展开图的基本概念

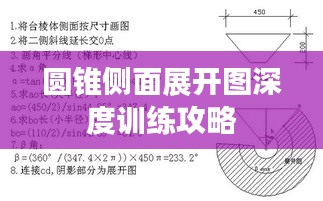
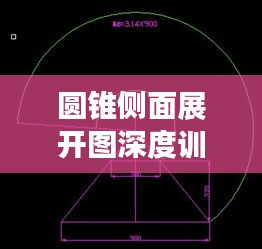
圆锥的侧面展开图是一个扇形，其半径等于圆锥的母线长度，弧长等于圆锥底面的圆周，掌握这一基本概念，是理解圆锥侧面展开图的基础。

专题训练

1、识别与绘制展开图：通过给出不同的圆锥，让学生识别其侧面展开图的形状，并尝试绘制。

2、计算扇形参数：给定圆锥的底面半径和母线长度，让学生计算侧面展开图所对应的扇形的半径和弧长。

3、展开图与圆锥的关系：通过改变展开图的形状或大小，观察对应的圆锥的变化，理解二者之间的关系。

4、立体图形与平面图形的转换：培养学生的空间想象力，使其能够实现在立体图形和平面图形之间的自由转换。

5、解决实际问题：通过给出实际生活中的例子，如灯塔、路标等具有圆锥形状的物体，让学生分析其侧面展开图的特征，并尝试解决问题。

训练方法与策略

1、理论与实践相结合：在理论学习的基础上，引导学生进行实际操作，如画图、制作模型等。

2、小组合作：鼓励学生进行小组讨论，通过合作解决问题，培养学生的团队协作能力。

3、个性化指导：针对学生的不同情况，提供个性化的指导，帮助学生解决学习中遇到的问题。

4、鼓励探索与创新：鼓励学生自主探索，创新解决问题的方法，培养学生的创新思维。

案例解析

以一道典型题目为例：给出一个圆锥的底面半径和母线长度，让学生求其侧面展开图所对应的扇形的半径和弧长，解题步骤如下：

1、根据给出的底面半径和母线长度，计算圆锥的侧面积和底面周长。

2、根据侧面展开图的概念，将圆锥的侧面积转化为扇形的面积，将底面周长转化为扇形的弧长。

3、根据扇形面积和弧长，计算扇形的半径。

通过本文的专题训练，学生应该能够更好地理解和掌握圆锥侧面展开图的相关知识，包括基本概念、计算方法、与圆锥的关系等，通过训练方法和策略的实施，学生的空间想象能力、数学思维能力、团队协作能力等也将得到培养和提高。

展望

在未来的学习中，学生还将接触到更复杂的几何体，如圆柱、棱柱等，学生需要继续加强几何体的侧面展开图的研究，提高空间想象能力和数学思维能力，为未来的学习打下坚实的基础。

1、加强对基本概念的理解：学生需要深入理解和掌握圆锥侧面展开图的基本概念，这是解题的基础。

2、多做练习：学生需要通过大量的练习，熟悉和掌握解题方法和技巧。

3、善于总结：学生需要善于总结自己的学习经验和方法，以便更好地提高自己的学习效率。

本文围绕“圆锥侧面展开图”进行了专题训练，希望通过本文的学习，学生能够更好地理解和掌握相关知识，提高空间想象能力和数学思维能力。